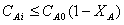Идеальные химические реакторы.

Эффективность любого химического процесса, выражаемая показателями производительности и селективности, в значительной степени определяется кинетической моделью процесса. В свою очередь характер этой модели определяет тип реактора, при котором достигается наиболее высокое значение указанных показателей. Наиболее удобно выявит влияние типа реактора на тот или иной процесс и его показатели на примере идеальных реакторов.

Классификация химических реакторов, основанная на структуре потока реакционной массы, различает идеальный реактор периодического действия, непрерывный реактор идеального вытеснения и непрерывный реактор идеального смешения.

Идеальный периодический реактор может быть представлен как емкостной аппарат, снабженный мешалкой, число оборотов которой обеспечивает равенство концентраций компонентов реакции в любой точке объема, 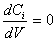 и постоянство температуры по объему ().

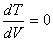Дополнительное условие идеальности такого реактора состоит в одновременной и моментальной загрузке всех компонентов исходной смеси.

Скорость протекания реакции 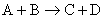 в таком реакторе во времени определяется выражением

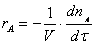                                                                                                                        (1)

Для периодических реакторов реакционный объем обычно постоянен и тогда уравнение (1) приобретает простой вид

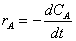                                                                                                                             (2)

Из последнего выражения следует, что

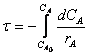                                                                                                                          (3)

Так как 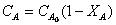, где Х_А – степень превращения компонента А, то

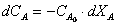
Уравнение (3) переходит в вид

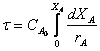                                                                                                                       (4)

Уравнение (4) является основой для расчета реакторов периодического действия. Оно справедливо для любого компонента простой и сложной реакции, причем для нахождения интеграла  надо подставить в него функцию .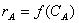

Задача 1.

Рассчитать реакционный объем периодического производства этилацетата с ежесуточной производительностью 50 т этилацетата в сутки.

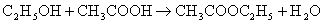
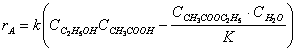, где k=7,93·10^{-6 м3} кмоль^-1 сек^-1, К=2,93.

Мольные скорости превращения каждого из компонентов равны вследствие равенства стехиометрических коэффициентов. Загружаемый водный раствор содержит 25 мас. % кислоты, 46 мас. % спирта и не содержит эфира. Степень превращения кислоты равна 35 %. Плотность реакционной массы постоянна и составляет r=1020 кг/м². Установка должна работать круглосуточно. Время загрузки, разгрузки и очистки реактора составляет 1 ч не зависимо от размеров реактора. Каков необходимый объем реакционной зоны, если использовать а) один реактор, б) три реактора?

Решение.

Основой для расчета является выражение 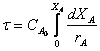                                               (1)

Рассчитаем концентрации компонентов реакционной массы в исходном растворе, исходя из объема 1 м³.

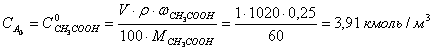
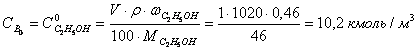
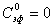
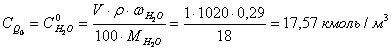
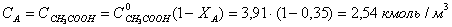
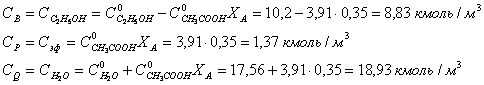
В соответствии с кинетическим уравнением скорость реакции выразится как

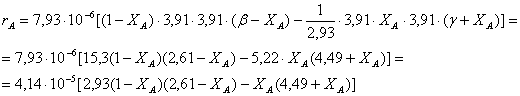
где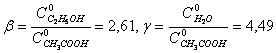

Подставляем окончательное выражение r_A в уравнение (1) и производим численное интегрирование полученной функции в пределах от Х=0 до Х=0,35.

В результате интегрирования получаем .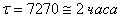

Время одной технологической операции составляет 2+1=3 часа. Таким образом, каждые 24 часа можно провести 24:3=8 операций.

Ежесуточное производство этилацетата на 1 м³ реакционного объема составляет

С_эф·М_эф·N_оп=1,37·88·8=965 кг                          

Тогда общий реакционный объем составит

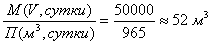
Таким образом, для обеспечения необходимой производительности необходимо использовать единичный реактор объемом 52 м³. Учитывая степень заполнения реактора 70 %, общий объем реактора составит 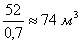. Согласно условию задачи, эту же производительность можно обеспечить тремя реакторами объемом .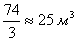

 

В непрерывном реакторе идеального вытеснения реакционная масса движется вдоль оси потока, вытесняя последующие слои. Условие идеальности такого аппарата состоит в том, что каждый элемент реакционной массы в данном поперечном сечении движется вдоль оси потока с одинаковой скоростью

 

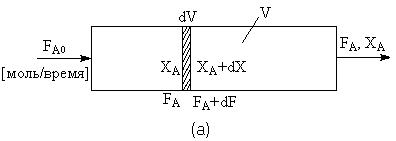В этой модели исключается торможение потока насадкой или стенками и диффузионные явления, из которых особенно существенно обратное или продольное перемешивание потока. При стационарном режиме работы, т.е. при постоянных во времени скорости, составе поступающей смеси и температуре, каждый элемент реакционной массы пребывает в реакторе идеального вытеснения одинаковое время, а концентрации реагентов и температура в каждом поперечном сечении остаются постоянными. В этом случае концентрации меняются только по длине аппарата, что позволяет составить дифференциальное уравнение материального баланса для элементарного объема dV в единицу времени

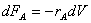
Интегрирование этого уравнения по всему реакционному объему V, когда количество вещества меняется от 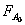 до F_A дает:

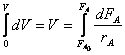                                                                                                                 (5)

Так как 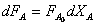, то это уравнение можно привести к виду

                                                                                                       (6)

или

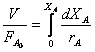                                                                                                                         (7)

Обратная величина левой части последнего уравнения 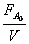 представляет собой удельную нагрузку реактора по реагенту А (число молей этого реагента в единицу времени на единицу реакционного объема).

Умножая обе части уравнения (7) на 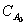, получаем

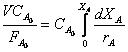                                                                                                                (8)

Сравнение полученного уравнения  с уравнением (4) для периодического идеального реактора показывает полную идентичность их правой части. В то же время выражение для левой части уравнения также имеет размерность времени, при этом величина 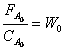 представляет собой объемную скорость реакционного потока на входе в реактор. Тогда левая часть представляет собой время контакта

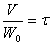
В этом случае уравнение (8) приобретает вид

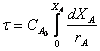                                                                                                                       (9)

полностью идентичный уравнению (4) для периодического идеального реактора. В общем случае величину контакта 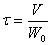 называют условным временем.

Задача 2.

Рассчитать объем реактора идеального вытеснения при тех же условиях, что и в предыдущей задаче.

Решение.

Принимаем, что время контакта в реакторе вытеснения такое же, что и в периодическом реакторе τ=7270 сек., мольная скорость потока продукта рассчитывается как

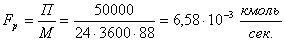
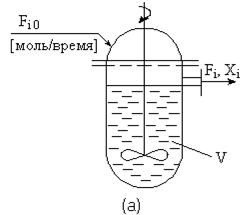Непрерывный реактор полного смешения (б) отличается тем, что в нем реакционная масса интенсивно перемешивается. Условием его идеальности является отсутствие градиентов концентраций и температуры по объему 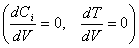, а при стационарном режиме концентрации и температуры постоянны и во времени. В таком аппарате концентрация вещества в исходной смеси С_{i 0} моментально падает (из-за разбавления в большом объеме реакционной массы до некоторой величины С_i, равной его концентрации в смеси, выходящей из реактора. Эта особенность реактора полного смешения дает возможность при стационарных условиях работы составить уравнение материального баланса в целом по аппарату (минус дифференциальные выражения)

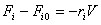                                                                                                                     (10)

Так как 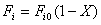, то 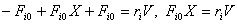, откуда следует, что

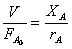                                                                                                                            (11)

Таким образом, в стационарном режиме работа реактора идеального смешения характеризуется алгебраическим уравнением. Реакторы идеального смешения называются безградиентными в отличие от интегральных реакторов периодического действия и идеального вытеснения, где концентрации и скорости реакций переменны – в первом случае во времени, во втором – по длине реактора, которая также пропорциональна времени реакции.

Умножая левую и правую части уравнения (11) на С_{А 0}

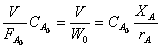                                                                                                      (12)

Если объем смеси во время проведения реакции не меняется, то

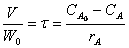                                                                                                              (13)

где τ – истинное время контакта.

Задача 3.

Емкость с полезным объемом в 52 м³, описанная в задаче 1, используется в качестве реактора непрерывного действия в режиме полного смешения. Состав загрузки и степень полного превращения уксусной кислоты составляет также 35 %. Какова производительность по этилацетату в это случае? Какой объем должен иметь реактор для производства 50 м³ этилацетата в сутки?

Решение.

В решении к задаче 1 были получены мольные концентрации при Х_А=0,35. Их можно использовать для расчета скорости реакции r_A.

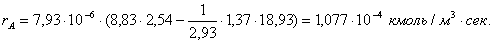
Тогда массовая скорость производства эфира

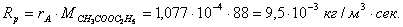
Общая скорость производства в реакторе 52 м³ составляет

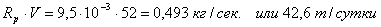
Для того чтобы обеспечить производительность 50 т/сутки, необходимо взять пропорционально больший реактор, т.е. 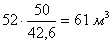, т.е. значительно больше, чем в случае реактора идеального вытеснения или идеального периодического реактора.

 

Сравнение эффективности проточных реакторов

идеального смешения и идеального вытеснения.

Сравним производительность идеальных проточных реакторов для случая проведения в них простых реакций, не осложненных побочными взаимодействиями. Зададимся одинаковой степенью превращения ключевого реагента и будем считать более эффективным тот реактор, для которого для достижения заданных результатов требуется меньшее время пребывания .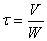

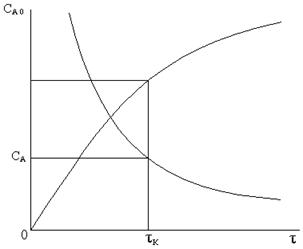
Для проточного реактора идеального смешения при заданной глубине превращения среднее время пребывания в соответствии с уравнением (13) можно определить как произведение двух постоянных величин

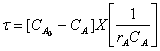
т.е. геометрически представить в виде прямоугольника с соответствующими сторонами.

Для стационарного реактора идеального вытеснения

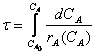
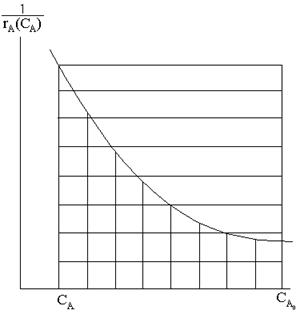
т.е. величина τ как определенный интеграл выражается геометрической площадью, ограниченной прямыми С_А и С_{А 0}, графиком функции 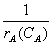 и осью абсцисс. Из рисунка видно, что площади, соответствующие времени пребывания в реакторе вытеснения, заметно меньше площади, соответствующей времени в реакторе смешения для достижения одного и того же результата. Следовательно, при равном объемном расходе реактор идеального вытеснения должен иметь меньший объем. Таким образом, реакторы идеального вытеснения характеризуются более высокой производительностью, чем реакторы идеального смешения.

Другим важным критерием эффективности реакторов является селективность процесса. Рассмотрев в этой связи ряд случаев, определяющих выбор в пользу реактора смешения или вытеснения.

1. Система параллельных реакций (основной и побочной), когда порядок побочной реакции по реагенту выше, чем основной

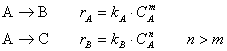
Рассмотрим кинетические зависимости для реагента А в реакторах смешения и вытеснения. Из этих зависимостей видно, что действующая концентраций в реакторе смешения С_А будет существенно ниже по сравнению со средней концентрацией А в реакторе вытеснения.

Это означает, что побочная реакция буде более успешно конкурировать с основной в реакторе смешения, т.е. селективность в этом реакторе буде ниже. Поэтому, если побочная реакция имеет более высокий порядок по реагенту, чем основная, то более выгодно для достижения более высокой селективности работать в реакторе смешения.

2. Система параллельных реакций (основной и побочной), когда порядок побочной реакции по реагенту ниже, чем основной, n<m. В этом случае большее значение эффективной концентрации в реакторе вытеснения обеспечит более успешную конкуренцию основной реакции по сравнению с побочной. В этом случае более высокая селективность будет достигнута в реакторе вытеснения.

3. Система параллельных реакций (основной и побочной), когда порядки основной и побочных реакций по реагенту одинаковы, m=n.

В этом случае выход целевого продукта не зависит от типа реактора.

4. Система последовательных реакций

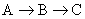
в которых В- основной продукт, С – побочный.

Очевидно, что в случае реактора смешения концентрация основного продукта в реакционной массе будет выше средней концентрации В в реакторе вытеснения. По этой причине в реакторе смешения скорость побочной реакции будет существенно выше, а селективность – ниже по сравнению с реактором вытеснения. Поэтому для достижения высоких селективностей последовательных реакций более выгодным является реактор вытеснения.

Таким образом, в ряде случаев для достижения высокого выхода целевого продукта эффективнее реактор идеального вытеснения, а иногда – реактор идеального смешения.

При выборе в пользу того или иного типа реактора необходимо также учитывать чисто эксплуатационные реакторы. К ним следует отнести большое гидравлическое сопротивление трубчатых реакторов, трудность чистки таких аппаратов. Реакторы смешения с интенсивным перемешиванием проще по конструкции и обеспечивают более эффективный подвод или съем тепла. В то же время они обладают низкой производительностью. Чтобы использовать преимущества реакторов смешения и вытеснения, используют каскад реакторов идеального смешения путем последовательного включения в технологическую нитку нескольких реакторов.

Каскад реакторов смешения.

Примером каскада реакторов является последовательная цепь емкостных аппаратов с мешалками.

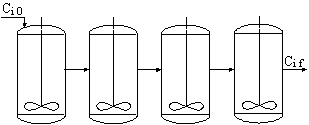Примером подобной модели может быть не только система последовательно расположенных отдельных аппаратов, но и проточный реактор тем или иным способом разделенный на секции, в каждой из которых осуществляется перемешивание реакционной смеси. В частности, близка к такому типу аппарата тарельчатая барботажная колонна.

Для каскада реакторов идеального смешения должны выполняться следующие допущения об идеальности.

1.      В каждой секции каскада выполняется условие реактора идеального смешения, т.е. мгновенное изменение параметров процесса, равенство параметров во всех точках секции и в потоке, выходящем из нее.

2.      Отсутствие обратного влияния: каждый последующий реактор не влияет на предыдущий.

Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому-либо участнику реакции, включающему по меньшей мере n Уравнений по числу секций каскада. Если составляется модель для сложной реакции, где недостаточно материального баланса только по одному участнику реакции, число уравнений математической модели кратно n.

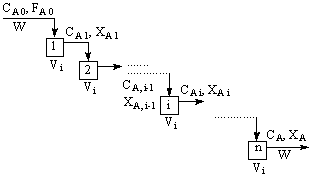Рассмотрим производительность каскада прямоточных реакторов полного смешения, взяв для примера простейшую реакцию первого порядка с участием реагента А.

Для каждого единичного реактора каскада можно записать в соответствии с уравнением (11)

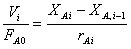                    (14)

Умножим обе части уравнения (14) на С_{А 0} и примем, что реакция идет без изменения объема, а все реакторы имеют одинаковый объем. Тогда имеем

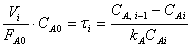, откуда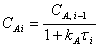

Соответственно, для первого и второго реакторов каскада

,

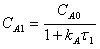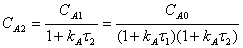
Очевидно, что для всей последовательности из n аппаратов (при 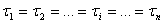) выражение будет следующим

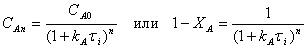                                                                  (15)

Суммарное время контакта 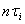 во всех реакторах общим объемом 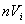 составит

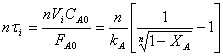
т.к. в соответствии с (15)

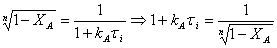
откуда следует .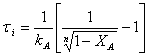

Отсюда производительность каскада (по реагенту А) равна

                                                                                                                  (16)

Так как 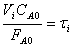, то .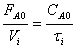

Подставляя последнее выражение в уравнение (16), имеем

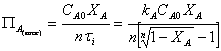
В то же время производительность единичного реактора вытеснения, заменяющего каскад,

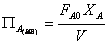                                                                                                                   (17)

Для реакции первого порядка, протекающей в реакторе идеального вытеснения в соответствии с уравнением (7)

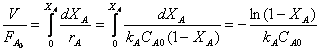
Подставляя 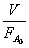 из последнего выражения в уравнение (17), имеем

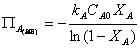
Тогда соотношение производительностей каскада реакторов смешения и РИВ

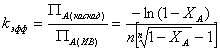
Значения относительной эффективности каскада для реакции 1-го порядка рассчитаны для разных n при Х_А=0,95.

n	1	2	4	8
kэфф	0,157	0,428	0,672	0,807

Можно видеть, что каскад из n реакторов идеального смешения значительно эффективнее, чем единичный реактор данного типа, причем с увеличением n каскад по удельной производительности все более приближается к модели идеального вытеснения. Это иллюстрируется кинетическими зависимостями для 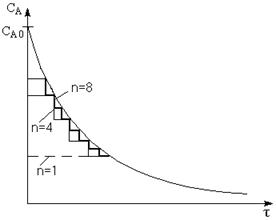каскада с различным n и РИВ.

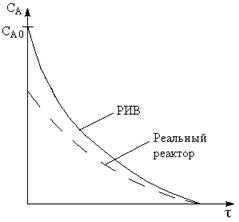
Если в реакторах вытеснения происходит частичное перемешивание реакционной массы, происходит выравнивание концентраций и скоростей по реакционному объему. В реальных реакторах такое выравнивание происходит в результате диффузии и конвекции. В этом отношении особенно нежелательна диффузия вдоль оси потока, называемая продольным (или обратным) перемешиванием, ведущая к более пологой кривой концентраций и снижению "средней" скорости и удельной производительности (см. ниже).

Из изложенного следует, что при непрерывном осуществлении гомогенных реакций всякое перемешивание реакционной массы, как правило, снижает удельную производительность реактора. Чтобы уменьшить эти нежелательные эффекты в реальных аппаратах, стараются увеличить отношение их длины (высоты) к диаметру, разделяют аппарат поперечными перегородками, исключают искусственное перемешивание и циркуляцию реакционной массы.

Из уравнения 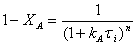 можно рассчитать число секций заданного объема, необходимых для достижения заданной степени превращения Х_А:

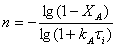                                                                                                                 (18)

Если полученное при расчете по уравнению (18) число n является дробным, то его округляют в большую сторону, чтобы было выполнено условие 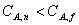, соответствующее числу секций в каскаде.

 

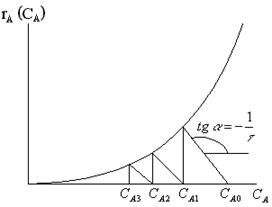Если возникает обратная задача определения числа секций, необходимого для достижения заданной степени превращения Х_А (С_А), графическое построение продолжают до тех пор, пока абсцисса точки пересечения прямой

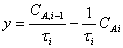
и кривой r_A (C_A) не будет соответствовать условию