Лекция 13.
Функция по состояниям в
классической и квантовой статистике. Большая сумма по состояниям.
Оглавление
Распределение
Максвелла по скоростям.
Функция по состояниям
Введем более широкое
понятие суммы по состояниям. При рассмотрении состояния системы в целом, как
функции состояния составляющих ее частиц, необходимо различать два случая:
различимость и неразличимость частиц.
Различимые частицы обладают
определенными характеристиками каждая; неразличимые – это группы частиц, в
которых характеристики частиц не отличаются друг от друга, в этом случае
свойства системы зависят только от числа частиц, распределенных в эти группы.
1.
Различимые частицы составляют систему
Максвелла-Больцмана, в которой состояние системы в целом характеризуется
указанием состояния каждой из N одинаковых частиц. Если обозначить
индексами i1, i2, i3, …iN состояния N
индивидуальных частиц, то при отсутствии взаимодействия между ними энергия
системы запишется как ![]() . Сумма по состояниям:
. Сумма по состояниям: ![]() , где ei – энергетическое состояние каждой молекулы, Q – сумма по состояния одной молекулы
(молекулярная сумма по состояниям).
, где ei – энергетическое состояние каждой молекулы, Q – сумма по состояния одной молекулы
(молекулярная сумма по состояниям).
При учете вырождения
(статистического веса) сумма по состояния z запишется в виде: ![]() , где gi – число
уровней, обладающих одинаковой энергией. Это выражения является суммой по
состояния системы Максвелла-Больцмана, состоящей из N различимых частиц, не
взаимодействующих между собой.
, где gi – число
уровней, обладающих одинаковой энергией. Это выражения является суммой по
состояния системы Максвелла-Больцмана, состоящей из N различимых частиц, не
взаимодействующих между собой.
2. Неразличимые частицы составляют газы типа Бозе-Эйнштейна
и Ферми-Дирака. Рассмотрим газ, состояние которого определяется просто
указанием числа частиц, находящихся в возможных различимых состояниях. Такой
способ рассмотрения указывает на возможность существования особых состояний
системы в целом, которые называются вырожденными. Вырождение этого типа
проявляется при низких температурах и высоких давлениях и тем легче, чем меньше
масса частиц. Оно ведет к тому, что при Т®0, ![]() . Этот тип вырождения рассматривается в квантовой статистике.
. Этот тип вырождения рассматривается в квантовой статистике.
Рассмотрим разряженный
газ из N невзаимодействующих частиц, каждая из
которых может находиться в общих для всех частиц состояниях: ek,el,em. Обозначим числа молекул в этих
состояниях Nk,Nl,Nm, тогда энергию системы из N молекул ЕN = e1 + e2 + e3 можно получить ![]() способами, просто
подставляя индексы от 1 до N у ei. В соответствии с суммой по
состояниям идеального газа, состоящего из N неразличимых элементов
способами, просто
подставляя индексы от 1 до N у ei. В соответствии с суммой по
состояниям идеального газа, состоящего из N неразличимых элементов 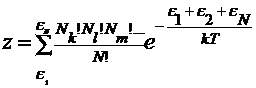 .
.
Применение данного
выражения возможно в двух случаях:
1. суммирование выполняется по всем
возможным значениям энергии от e1 до eN в статистике Бозе-Эйнштейна, разработанной Бозе для световых квантов и распространенной Эйнштейном на
молекулы и газы.
2. применяется принцип Паули, согласно
которому исключаются члены, в которых два или большее число значений энергии ei (i = 1,2…N) относятся к одному и тому же состоянию, тогда
говорят о статистике Ферми-Дирака, разработанной для электронного газа.
Выражение
z можно упростить, применяя его к газу при высокой температуре
и большом объеме. При большом числе энергетических состояний можно допустить,
что на каждый из них приходиться не более одной молекулы, тогда Nk,! Nl,! Nm!...= 1 и 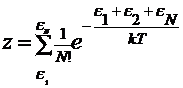 или с учетом
вырождения
или с учетом
вырождения 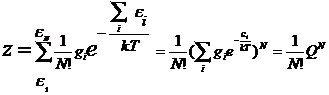 .
.
Сравнивая
выражения z в статистике Максвелла-Больцмана и
выражение z в статистике Бозе-Эйнштейна
и Ферми-Дирака, видим, что выражения отличаются только множителем ![]() . Обычно при расчетах пользуются ln z = N ln Q – ln N! , где по
Стирлингу ln N! = N ln N – N + ½ ln 2p N , тогда ln z = N ln Q – N ln N + N - ½ ln 2p N = N (ln Q – ln N + 1) –
. Обычно при расчетах пользуются ln z = N ln Q – ln N! , где по
Стирлингу ln N! = N ln N – N + ½ ln 2p N , тогда ln z = N ln Q – N ln N + N - ½ ln 2p N = N (ln Q – ln N + 1) –![]() ln 2p N ,
при N®¥ ln z = N ln(
ln 2p N ,
при N®¥ ln z = N ln(![]() ) –
сумма по состояниям z в отличии от молекулярной суммы по
состояниям называется большой суммой по состояниям.
) –
сумма по состояниям z в отличии от молекулярной суммы по
состояниям называется большой суммой по состояниям.
Распределение Максвелла по скоростям.
На основе закона Бозе, примененного к одноатомному идеальному газу для
поступательного движения частиц вдоль координаты x,
вероятность обладания скоростью, лежащей в пределах ![]() и
и ![]() - закон распределения
молекул по скоростям при одномерном движении.
- закон распределения
молекул по скоростям при одномерном движении.
 На основании вычисления средних
значений средняя скорость движения молекул в одном направлении
На основании вычисления средних
значений средняя скорость движения молекул в одном направлении ![]() будет равна
будет равна 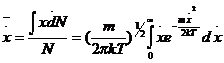 или
или ![]() . При движении в трехмерном пространстве вероятность
обладания скоростью вдоль направления
. При движении в трехмерном пространстве вероятность
обладания скоростью вдоль направления ![]() при
при
![]() будет
равна произведению трех одинаковых вероятностей вида
будет
равна произведению трех одинаковых вероятностей вида ![]() - уравнение Максвелла
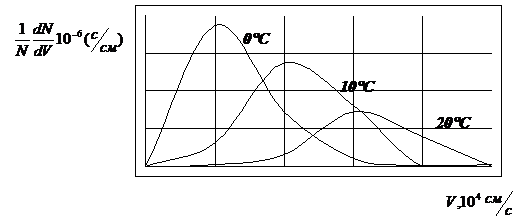
для распределения молекул по скоростям. Графически функция распределения
Максвелла выражается:
- уравнение Максвелла
для распределения молекул по скоростям. Графически функция распределения
Максвелла выражается:
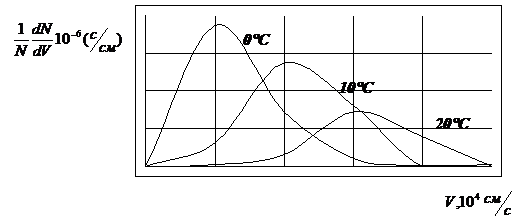
Максимум этой функции соответствует
наиболее вероятной скорости движения молекул.
Средняя скорость будет
равна 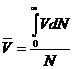
Средняя квадратичная
скорость равна: ![]() , т.к.
, т.к.
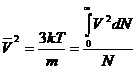 при
при ![]() получаем более компактное
выражение для расчета параметров кинетической теории газов:
получаем более компактное
выражение для расчета параметров кинетической теории газов:
![]() ,
, ![]() ,
, ![]() ,
, ![]()