Лекция 20.
Вычисление
термодинамических функций. Статистические расчеты колебательных равновесий.
Межмолекулярный потенциал.
Оглавление
В основе расчета констант химического
равновесия лежат основные термодинамические соотношения. Задача статистической
термодинамики выразить химический потенциал компонентов через соответствующую
сумму по состояниям.
Условием химического равновесия в
смеси идеальных газов является равенство сумм химических потенциалов исходных
веществ и продуктов реакции. Для того чтобы выразить константу равновесия в
смеси идеальных газов через сумму по состояниям необходимо получить выражение
для химического потенциала. Полная сумма по состояниям смеси связана с
молекулярными суммами по состояния 
следующим образом: 
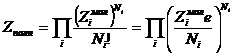в соответствии с этим
энергия Гельмгольца принимает вид: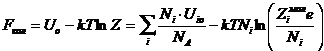 
.
Химический потенциал i – компонента:
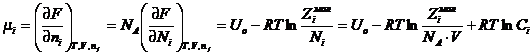, где 
, 
.
Для химической реакции в газовой фазе
характерен переход от 
к
. Условия равновесия: 
=
. Подставляя в это равенство предыдущее выражение для m
исходных веществ и продуктов реакции, получим константу равновесия: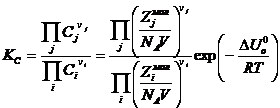 
,
где 
, т.е. тепловой эффект реакции при абсолютном нуле.
Полученное уравнение является базовым
в статистической теории химического равновесия. Другие константы равновесия
можно выразить через 
с
использованием уравнения идеального газа: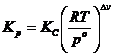 
.
Статистическая термодинамика реального газа и конденсированного состояния
вещества. Сумма по состояниям реальных газов.
Основные
термодинамические функции U, F, S, H, G, CV, выраженные через сумму по
состояниям, устанавливают связь между термодинамикой и статистической механикой
и выражения их справедливы для любых термодинамических систем.
Для классических систем в
которых квантовый эффект несущественен, например для систем, состоящих из
частиц, не имеющих внутренней структуры, справедливо выражение суммы по
состояниям в виде: 
. Многие такие классические системы газов и жидкостей
описываются функциями Гамильтона вида: 
, m – масса частицы, 
- потенциальная
энергия их взаимодействия. В этом гамильтониане координаты q и импульс р разделены и поэтому
интегрирование можно провести независимо, подставляя выражение в предыдущее и
вычисляя интеграл по N и р.
Полную статистическую сумму по состояниям реального газа или жидкости можно
представить в ви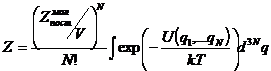де:
, где 
- сумма по состояниям
одной частицы, V – объем.
Интеграл по координатам в
данном выражении называют конфигурационным
интегралом 
.
Конфигурационный интеграл
определяет зависимость суммы по состояниям от объема и содержит в себе описание
всех отклонений системы от идеальности. Давление системы определяется только
конфигурационным интегралом: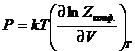 
.
Точный теоретический расчет статистической суммы по состояниям газов или
жидкостей с произвольным гамильтонианом H(p,q) – задача, которая лежит далеко за пределами
возможностей современной статистической теории. Однако статистическую сумму по
состояниям и конфигурационный интеграл для реальных газов, состоящих из
валентно насыщенных молекул можно оценить, если сделать ряд приближений.
Главное
приближение.
Общая внутренняя энергия
взаимодействия частиц может быть
представлена в виде суммы парных потенциалов, каждый из которых зависит только
от расстояния между частицами 
, 
. Для того чтобы конфигурационный интеграл с потенциалом 
сходился, нужно чтобы
парный потенциал при больших расстояниях быстро стремился к 0. Это требование
выполняется для большинства газов. Некоторые модельные парные потенциалы,
которые используют при расчете свойств реальных газов определены
опытным путем и сведены в таблицы, и называются межмолекулярными потенциалами.
Выражение потенциала Сазерленда:
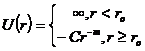См. диаграмму полной колебательной энергии.
Выражение потенциала EXP-6: 
.
Расчет конфигурационного
интеграла в приближении парных потенциалов дает следующее выражение:
(*) , где V – объем, b - вириальный коэффициент, который
определяется через межмолекулярный потенциал U(r):
.
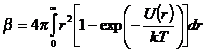Для плотных газов, в которых
учитываются возможные конфигурации, сложный расчет конфигурационного интеграла
в приближении парных потенциалов приводит к следующему выражению:
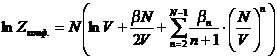. Здесь
параметры bn называют групповыми интегралами, они описывают конфигурации,
в которых образуются группы из (n+1) частиц. Для слабо разряженных газов
можно записать уравнение состояния, которое вытекает из уравнения (*),
т.к. 
зависит только от V. Такое
уравнение состояния имеет вид:
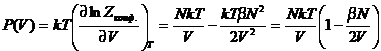. Если
сравнить это уравнение с вириальным уравнением идеального газа, то можно найти
статистическое выражение для второго вириального коэффициента реального газа:
.
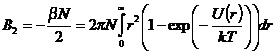Температурная зависимость этого
коэффициента при заданной функциональной форме межмолекулярного потенциале
позволяет определить параметр этого потенциала.
Для получения уравнения состояния
сжатого реального газа необходимо использовать второе выражение
конфигурационного интеграла. Дифференцируя по dV найдем вириальное разложение:
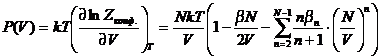. Из
этого уравнения следует общее выражение для всех вириальных коэффициентов через
групповые интегралы: 
.
Если уравнение Ван-дер-Ваальса
привести к виду вириального уравнения, то оно запишется как уравнение со вторым
и третьим вириальным коэффициентом.
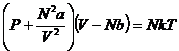- уравнение Ван-дер-Ваальса в обычной форме
для газа из N частиц.
, где 
, 
.
Для модели
Сазерленда справедливы сотношения: при ro £ r U(r) = ¥,
f(r)=1
при ro ³ r, 
, 
для 
и для
статистического уравнения состояния в виде уравнения со вторыми вириальными
коэффициентами будет: 
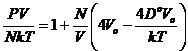. Данное уравнение можно использовать для интерпретации постоянных в уравнении Ван-дер-Ваальса в вириальной форме
следующим образом: a = 4DoVo, b = 4Vo при Vo ® ro
