Лекция 3

 

 

Второе начало термодинамики.

Энтропия и методы её определения.

 

План

 

1.     Внутренняя неупорядоченность макросистемы и термодинамическая температура.

2.     Второе начало термодинамики.

3.     Третье начало термодинамики.

4.     Термодинамические потенциалы, как критерии самопроизвольного протекания процесса.

 

По величине внутренней энергии и энтальпии нельзя судить находится ли данная система в равновесном состоянии  или нет, а также ничего нельзя сказать о возможности протекания процессов в этих системах. Поэтому для этой цели нужна другая функция состояния, которая может служить критерием самопроизвольного протекания необратимых процессов.

Наиболее характерной чертой всякого макроскопического тела является то, что пространственное расположение и движение образующих его микрочастиц в большей или меньшей степени являются беспорядочными. Это беспорядочное расположение частиц в макротеле создается само собой, тогда как упорядоченное в хаотическом  расположении частиц требует затраты работы. В идеале, за количественную меру беспорядка в системе сложно взять работу по «наведению» идеального порядка. Однако можно дать и более общее и более точное определение меры беспорядка в системе, не требующее её перевода в идеально упорядоченное состояние.

Количественная мера внутренней неупорядоченности системы в термодинамике называется энтропией-S. Произвольное макротело изолированное от среды в силу атомно-молекулярной природы по истечению какого-то времени само собой придет в состояние термодинамического равновесия и будет прибывать в нем сколь угодно долго. С точки зрения внутренней неупорядоченности, всякий процесс релаксации – это переход от состояния с большей упорядоченностью в состояние с меньшей упорядоченностью. В изолированной системе этот процесс ограничен пределами, когда достигается максимальная неупорядоченность, поэтому процесс релаксации  в изолированной системе всегда ведет к росту энтропии. Это общее свойство энтропии любых макроскопических тел, находящихся в изоляции, называется принципом максимума энтропии.    

В термодинамике, с её феноменологическим подходом, величина энтропии введена формально. Связь энтропии с мерой внутренней неупорядоченности макротел была установлена позднее в статистической механике.

Увеличение  энтропии  - это результат неравновесности протекания процесса, который сопровождается рассеиванием энергии. Чем больше рассеивается энергии, тем больше применение энтропии.

Если в системе протекает обратимый процесс, то внутренняя неупорядоченность закрытых систем может меняться только тогда, когда система обменивается энергией со средой в форме теплоты, а не в форме работы. Если система поглощает энергию из вне и получает ее в форме теплоты, то возрастают одновременно 2 термодинамические функции, внутренняя энергия  и энтропия. Таким образом, внутренняя энергия является монотонно возрастающей функцией энтропии. Следовательно, для простых равновесных систем:

 

                               U = U (V,S)                                       (3-1)

 

         Для (3-1) мы можем найти полный дифференциал внутренней энергии.

 

                             dU = ()_S * dV + ()_V  * dS                             (3-2)

 

Если сопоставить уравнение (3-2) с выражением 1–го начала термодинамики:

 

                           dU = dQ – pdV                                     (3-3)

 

то можно заметить:

 

()_V  * dS  = dQ, а ()_S = - p

 

         Обратим внимание на то, что ()_V обладает всеми признаками температуры, поэтому ()_V = Т, а (3-3) можно записать

 

                                  dU = TdS – pdV                                              (3-3^` ) 

 

Второе начало термодинамики.

 

         Ф. Кларуфиус, на основе анализа работы тепловой машины, работающей по циклу Карно, показал, что для обратимых процессов в макросистемах приведенная теплота обладает свойствами функции состояния:

                                           dS =                                                    (3-4)

 

         Эта функция состояния интересна тем, что равенство (3-4) выполняется только для обратимых процессов, а в случае необратимых процессов имеет место неравенство:

 

                                                     dS >                                                        (3-4`)

 

         Соотношения (3-4) и (3-4`) представляют общую формулировку второго начала термодинамики в аналитической виде: дифференциал энтропии не убывает.

         Рассмотрим важнейшие следствия из этой общей формулировки:

         1. Второе начало термодинамики позволяет определить изменение энтропии на основании калориметрических данных. Таким образом, энтропия, как и энтальпия и внутренняя энергия является термической константой.

         Действительно,

 

            ∆ S_(p) = 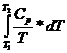 = 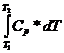lnT                               (3-5)

 

а для фазовых переходов (плавление, испарение):

 

            ∆ S_(p) =                                        (3-6)

 

         2. При адиабатической изоляции применение энтропии не отрицательно.

 

                                   Q = 0 → ∆ S  0                                             (3-7)

 

Это служит критерием самопроизвольного процесса в адиабатической системе.

3. Соотношение (3-7) справедливо для любых изолированных систем. Поэтому можно сформулировать энтропийный принцип: энтропия изолированной системы при протекании в ней обратимых процессов не изменяется, а при протекании необратимых процессов – возрастает.

 

Третье начало термодинамики.

 

II второе начало термодинамики позволяет определить только применение энтропии тел. Однако, обширный материал экспериментальных работ В. Нернста и других исследователей позволил сделать вывод, что при понижении температуры энтропия уменьшается. Причем, чем ближе температура а 0 К, тем ниже энтропия. Этот факт лежит в основе третьего начала термодинамики. При равновесном приближении к абсолютному нулю температуры энтропия макроскопических тел стремится к нулю.

                                       S = 0                                               (3-8)

         Соответственно при  неравновесном понижении температуры система остается в «замороженном» метастабильном состоянии. Причем, это фактически неизбежно в реальном опыте. По мере понижения температуры, возрастает время релаксации до бесконечности. Поэтому из III начала термодинамики вытекает в качестве следствия принцип недостижимости  абсолютного нуля температур.

         Другим важным следствием третьего начала термодинамики является заключение о характере температурной зависимости теплоемкости при температурах, близких к 0 К. Это позволяет определять абсолютные энтропии.

 

Термодинамические потенциалы

 

         Рассмотрим следствия, вытекающие из совместного применения I и II начала термодинамики к произвольной системе, взаимодействующей с окружающей средой:

 

                                     TdS   = dU +                            (3-9)  

   

I начало термодинамики применимо как к обратимым, так и к необратимым процессам. Однако, при замене ∂Q на TdS для необратимых процессов выполняется неравенство.

         Предположим в системе совершается работа связанная с действием различных сил не связанных с механической работой, то выражение для этого случая в необратимых процессах выражается:

 

                                 - > dU + pdV - TdS                                 (3-10)

 

Из (3-10) следует:

1) при V = const, S = const          - > dU

2) при  p = const, S = const          - > dU + pdV = d (U +pV) = dH    

3) при  p = const, T= const         - > dU + dpV – dTS = d (U + pV - TS)=          = d (H - TS)

4) при V = const, T= const        - > dU – TdS = dU – dTs = d (U - TS)

         Исходя из выражения (3-10) с учетом того, что самопроизвольный процесс – это процесс который сам способен производить положительную работу, то для случаев 1) - 4) можно записать условия самопроизвольного протекания необратимого процесса:

 

                                                     d П_(x,y)  <  0                                                (3-11)

 

         где П_(х,у)  это U_(V,S) или Н_(Р,S)  или выражения под знаком дифференциала для случаев 3), 4). Эти функции получили специальное название, потому что они имеют практический интерес (свободная энергия Гиббса (G) и Гельмготца F))

 

                                       G = H – TS                                                (3-12)

                                       F = U – TS                                                 (3-13)

 

         Очевидно, что  ∆G_(P,T)  и ∆F_(V,T) могут быть определены из эксперимента, поскольку обеспечить р=соnst и Т= соnst или V= соnst и                 Т= соnst в эксперименте не представляет труда.

         Выражение (3-11) определяет фактически направленность необратимого процесса: при самопроизвольном процессе убывает термодинамический потенциал. 

         Итак, нами установлено, что

 

П_{(х,у) =}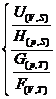

 

Все эти функции при постоянстве своих естественных переменных убывают при самопроизвольном необратимом процессе и служат критерием направленности этих процессов.

         У этих функций своим естественным переменным есть еще одно замечательное свойство. Взяв производные от этих функций по естественным переменным можно выразить все термодинамические параметры, т.е. охарактеризовать термодинамическую систему в целом. Поэтому все термодинамические потенциалы являются характеристическими функциями. Поскольку  с точки зрения математики безразлично, что взять в качестве аргумента, то очевидно характеристической функцией может быть и V = f (U,S) = ψ (F,Т) или температура Т = ψ (G,Р) = ψ (F,V). Поэтому, строго говоря, характеристическая функция – это более общее понятие, чем термодинамический потенциал. 

 

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f  (p, Т, V) = 0                                              (1)

 

 

                                                  рV = n R T                                              (1.2)

 

                            δQ = dU + δA                                      (1.3)

 

                                    Q = ∆U + A                                         (1.3′)

 

 

Q = ∆U + p ∆V + A′ = ∆U + ∆ pV + A′ = ∆ (U + pV) + A′                  (1.4)

 

 

                                                     Н = U + pV                                                 (1.4′)

 

         Из выражения (1.4) следует, что при  A′ = 0:

 

                                                Q_V  = ∆U, а Q_p  = ∆H                                       (1.5)