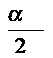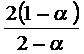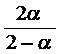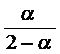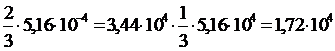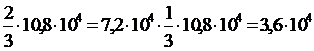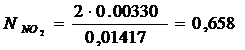ЛЕКЦИЯ
6
Химическое равновесие
План лекции:
1.
Закон действующих масс. Различные способы
выражения константы равновесия для идеальных систем.
2.
Связь константы равновесия с применением энергии
Гиббса. Уравнение изотермы химической реакции.
3.
Зависимость константы равновесия от температуры.
Уравнение изобары химической реакции.
4.
Понятия для активности и летучести (фугитивности).
Большинство химических реакций протекают одновременно в двух
направлениях: в сторону образования продуктов реакции (прямая реакция) и в
сторону разложения последних (обратная реакция). Вследствие химической обратимости
реакции не доходят до конца. Скорость прямой реакции уменьшается, а скорость
обратной, напротив, возрастает. Когда эти скорости выравниваются наступает
состояние химического равновесия.
Так как химически обратимые реакции до перехода в
равновесное состояние протекают с конечными скоростями, то с точки зрения
термодинамики они не обратимы. Однако можно мысленно представить, что эти
реакции идут бесконечно медленно через смежные равновесные состояния. Тогда к
ним можно применить общие условия термодинамического равновесия.
Для гомогенных обратимых
реакций экспериментально Гульбергом и Ваге был установлен закон действующих
масс. При постоянной температуре отношение произведения равновесных
концентраций (или парциальных давлений) продуктов реакции к произведению
равновесных концентраций (или парциальных равновесий) исходных веществ есть величина
постоянная.
Этот экспериментально установленный закон может быть получен
методом термодинамических потенциалов. Рассмотрим реакцию в газовой фазе:
аА(г) + bВ ↔
сС + dD
Когда система достигает термодинамического равновесия, то
термодинамический потенциал при фиксированных естественных переменных достигает
минимума. Равновесие, таким образом, можно охарактеризовать выражением
химических потенциалов, когда потенциалы продуктов реакции сравняются с
потенциалами исходных веществ:
с μ (с) + d μ (D) – a μ (a) - b μ (b) = 0 (6 – 1)
Если естественными переменными являются p и T, то ![]() =
= ![]() , а
, а  = V
= V
Отсюда для систем,
подчиняющихся закону идеальных газов, можно получить выражения для μi
μi = μi° + RTlnCi (6 – 2)![]()
где μi° - стандартный химический потенциал.
Подставляется
(6 – 2) в (6 – 1) и перенося постоянные величины в левую часть, получаем
сμC° + dμD° - aμA° - bμB° = -RTln![]()
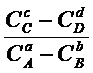 (6 – 3)
(6 – 3)
Поскольку
в левой части выражение не зависит от концентраций, то выражение под логарифмом
является постоянной величиной при постоянной температуре:
![]()
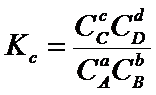
Для
идеального газа парциальные давления пропорциональны концентрациям, поэтому
константа равновесия может быть всегда выражена через равновесные парциальные
давления:
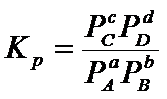
Аналогично
может быть записано выражение через мольные доли:
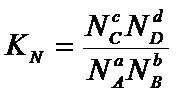
Для
идеальных газов эти константы связаны между собой соотношением:
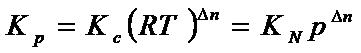
где ![]()
Следует
обратить внимание, что в полученных соотношениях только KN зависит от общего давления. Она позволяет нам
оценивать сдвиг равновесия в газовых реакциях при изменении общего давления. Следует
иметь в виду, что давление в этих выражениях складывается из парциальных
давлений компонентов системы и не учитывает влияние инертных газов, если они
присутствуют в реакционной смеси. Естественно инертный газ «разбавляет»
компоненты реакционной смеси и поэтому влияет на KN.
Из уравнения (6
– 3) вытекает связь константы равновесия с ∆rG°:
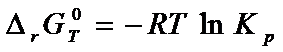 (6
– 4)
(6
– 4)
Это
уравнение было впервые получено Вант – Гофором методом циклов и получило
название уравнения изотермической химической реакции. Очевидно, в этом
уравнении ∆rGT° относится к этой температуре,
при которой определена Кр. Уравнение изотермической химической реакции
позволяет определить константу равновесия при заданных условиях не прибегая к
исследованию равновесия. Величина ∆rGT° может быть рассчитана на основе термических констант
для индивидуальных веществ.
Если
заданы концентрации (парциальные давления) отличные от равновесных, то можно
записать более общий вид уравнения изотермической химической реакции:
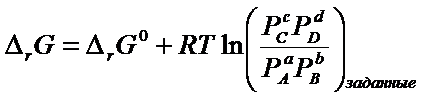
Это
выражение позволяет определить направление самопроизвольного процесса.
Уравнение
изотермы химической реакции позволяет получить выражение для температурной
зависимости константы равновесия.
Запишем
уравнение Гиббса – Гельмгольца:
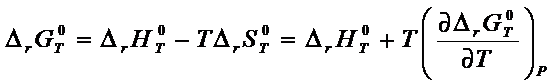
Подставим
выражение для ![]() из (6 – 4)
из (6 – 4)
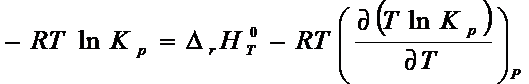 (6 - 5)
(6 - 5)
Дифференцируем уравнение (6 – 5)
![]()
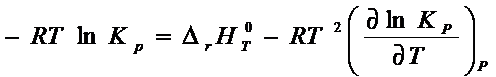 (6 -
5´)
(6 -
5´)
Из
уравнения (6 - 5´) получаем уравнение изобары химической реакции:
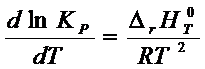 (6 – 6)
(6 – 6)
Если
проинтегрировать уравнение (6 – 6) в
предположении, что ∆rHT° не зависит
от температуры, то получим уравнение:
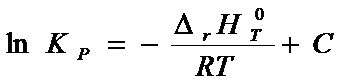
где С – константа интегрирования.
Уравнение (6 – 7) хорошо выполняется в узких
интервалах температур и позволяет определить ∆rGT°.
Для широких интервалов температур ln Kр представляют в виде степенных рядов или других
аналитических формах:
Например:
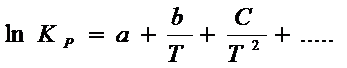
Такие выражения позволяют рассчитать все
термодинамические функции для процессов, для которых данные зависимости
получены.
Выражения для термодинамических потенциалов,
полученные для идеального газа. Для реальных газов, а особенно для газовых
растворов возникают затруднения. Это связано с тем, что расчет концентраций и
давлений должен быть проведен исходя из уравнения состояния. Однако для
реальных систем единое достаточно простое уравнение состояния получить не
удалось.
В связи с этим в термодинамике реальных систем
применяется эмпирический метод, предложенный Льюисом. Льюис предложил в
уравнениях термодинамики, полученных для идеальных систем заменить давления p на величину летучести f, а концентрации С на активности a.
При такой замене выражения для констант равновесия не
меняются по форме. Но этот прием позволяет связать экспериментально найденные
свойства реального газа с термодинамическими параметрами.
Летучести и активности – это экспериментальные величины, которые
находятся из условия, что для раствора при бесконечном разбавлении или газа при
давлении стремящимся к 0 активность приближается к аналитической концентрации,
а летучесть к реальному давлению идеального газа. Исходя из этой посылки рассчитываются
активности и летучести.
Пример 6
– 1.
При 1273 К и общем равновесии 30 атм. В равновесной
системе
![]() содержится 17% (по
общему)
содержится 17% (по
общему) ![]() . Сколько процентов
. Сколько процентов ![]() будет содержаться в
газе при общем давлении 20 атм.? При каком давлении в газе будет содержаться
25%
будет содержаться в
газе при общем давлении 20 атм.? При каком давлении в газе будет содержаться
25% ![]() ? (Газ считать идеальным).
? (Газ считать идеальным).
Решение.
В соответствии с законом Авогадро, объёмный процент
равен мольному проценту. Следовательно, ![]() при 30 атм. будет равен:
при 30 атм. будет равен:
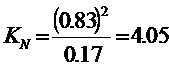
Отсюда находим ![]()
![]()
В отличие от ![]() ,
, ![]() для идеальных газов не зависит от давления. На основании
этого находим
для идеальных газов не зависит от давления. На основании
этого находим ![]() при 20 атм.
при 20 атм.
![]()
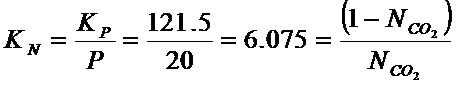
![]() = 0,125 или 12,5%
= 0,125 или 12,5%
Для 25% ![]()
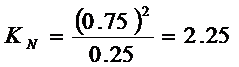
Следовательно, ![]()
Пример 6
– 2.
При 2000°С и общем давлении 1 атм. 2% воды
диссоцииовано на водород и кислород. Рассчитайте константу равновесия реакции 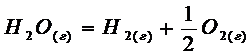 при этих условиях.
при этих условиях.
Решение.
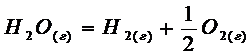
|
Исходное
количество |
1 |
0 |
0 |
|
Равновесное
количество |
|
|
|
|
Равновесная
мольная доля |
|
|
|
Следовательно, 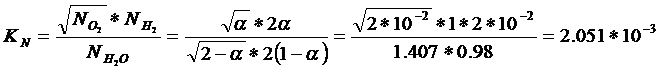
![]()
Пример 6 – 3
Константа равновесия реакции ![]()
При 500°С равна ![]() Смесь, состоящую из 1 моля СО и 5 моль
Смесь, состоящую из 1 моля СО и 5 моль ![]() нагрели до этой температуры. Рассчитайте мольную долю
нагрели до этой температуры. Рассчитайте мольную долю ![]() в равновесной смеси.
в равновесной смеси.
Решение.
![]()
|
Исходное
количество |
1 |
5 |
0 |
0 |
|
Равновесное
количество |
1 - х |
5 - х |
х |
х |
Поскольку
![]() , то
, то ![]()
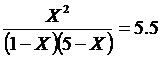 , следовательно, Х = 0.96
, следовательно, Х = 0.96
Следовательно,
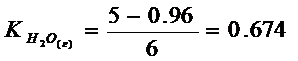
Пример 6 – 4.
Рассчитайте стандартную
энтальпию реакции, для которой константа равновесия
а) увеличивается в 2 раза,
б) уменьшается в 2 раза,
при изменении температуры от
298 К до 308 К.
Решение.
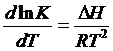 , после интегрирования получаем
, после интегрирования получаем 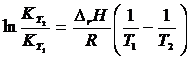
или 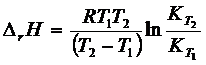
а) ![]() Дж∙мольˉ¹
Дж∙мольˉ¹
б) ![]() Дж∙мольˉ¹
Дж∙мольˉ¹
Пример 6 – 5.
Оксид
ртути диссоциирует до реакции ![]()
При 420°С давление газов ![]() Па, а при 450°С
Па, а при 450°С ![]() Па. Рассчитайте константы равновесия при этих температурах и
энтальпию диссоциации HgO.
Па. Рассчитайте константы равновесия при этих температурах и
энтальпию диссоциации HgO.
В соответствии с уравнением реакции.
![]()
|
Исходное количество
газообразных продуктов |
- |
0 |
0 |
|
Равновесное количество
газообразных продуктов |
- |
2 |
1 |
|
Мольные доли газообразных
продуктов |
- |
|
|
|
Парциальные давления газообразных
продуктов при 420°С, Па |
|
|
Парциальные давления газообразных
продуктов при 450°С, Па |
|
![]()
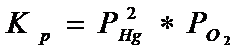
За стандарт принят ![]() , поэтому
, поэтому ![]()
![]()
Рассчитываем ![]()
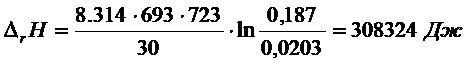
С
учетом того, что диссоциирует 2 моля HgO,
энтальпия диссоциации HgO составляет
154 кДж∙мольˉ¹.
Следует обратить внимание на то, что если ![]() рассчитывать исходя из ранее принятого стандартного давления
= 1атм., то их значения будут отличаться:
рассчитывать исходя из ранее принятого стандартного давления
= 1атм., то их значения будут отличаться:
![]()
![]()
Пример 6 – 6:
Зависимость константы
равновесия реакции ![]() от температуры между
300К и 600К описывается уравнением:
от температуры между
300К и 600К описывается уравнением:
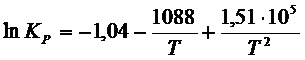
Рассчитайте ![]() ,
, ![]() и
и ![]() реакции при 400 К.
реакции при 400 К.
Решение:
По
уравнению изотермы химической реакции: ![]()
Отсюда находим
непосредственно температурную зависимость ![]()
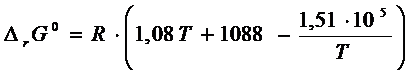
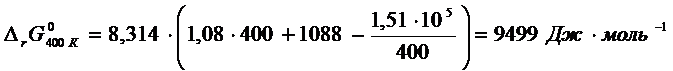
Для расчета ![]() удобнее
продифференцировать
удобнее
продифференцировать ![]() по
по ![]() . В этом случае
. В этом случае 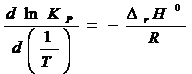 . Отсюда
. Отсюда 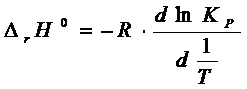
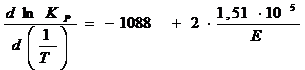
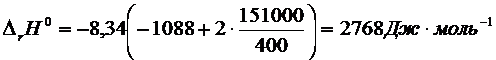
Расчет ![]() проводим на основании
уравнения Гиббса - Гельмгольца:
проводим на основании
уравнения Гиббса - Гельмгольца:
![]()
![]()
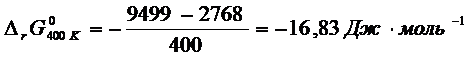
Пример 6 – 7:
Рассчитайте
константу равновесия реакции ![]() , если известно, что при получении жидкого формальдегида
, если известно, что при получении жидкого формальдегида ![]() при 198 К, а давление
пара формальдегида при этой температуре равно 1500 Торр.
при 198 К, а давление
пара формальдегида при этой температуре равно 1500 Торр.
Решение:
Имеем
следующие данные:
![]()
![]()
![]()
![]()
Из
этого следует, что ![]() при получение газообразного формальдегида складывается из
этих величин:
при получение газообразного формальдегида складывается из
этих величин:
![]()
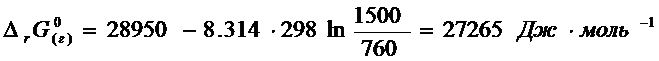
Отсюда 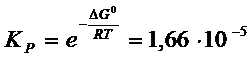
Пример 6 – 8:
Константа равновесия
реакции ![]() при 25°С равна
при 25°С равна ![]() , рассчитайте давление, которое установится в сосуде 1л,
содержанием 1г.
, рассчитайте давление, которое установится в сосуде 1л,
содержанием 1г. ![]() при этой температуре.
при этой температуре.
Решение:
![]()
|
Исходные концентрации моль∙¹ |
|
0 |
|
Равновесные концентрации моль∙¹ |
|
2Х |
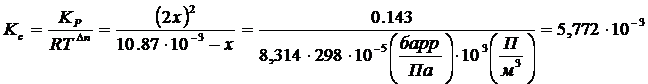
|
Х = 0,00330 |
|
|
∑=0,01417 |
|
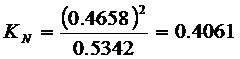
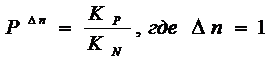
![]()