Химическое равновесие. Общее термодинамическое условие рав­новесия и их выражения через характеристические функции. Работа химической реакции. Три способа ее определения. Третий закон термодинамики. Абсолютная энтропия и вычисления энтропии твердых, жидких и газообразных тел. Изотерма Вант-Гоффа.

Состояние системы, которое характеризуется равенством скоростей прямой и обратной реакции и постоянством концентрации всех веществ называется химическим равновесием.

mA + nB = pC + qD

Константа равновесия зависит от природы веществ и температуры и не зависит от исходных концентраций. В небольших количествах (1 – 2 атм) давление на константу равновесия не влияет.

DG^o = – RTln(K_равн.)

Изменение константы равновесия с температурой определяется изменения энтальпии. Если DН < 0, то с увеличением температуры константа равновесия уменьшается. Если DН > 0, то с увеличением температуры константа равновесия увеличивается.

Смещение равновесия.

Смещение равновесия – переход системы из одного равновесного состояния в другое при изменении внешних условий.

Принцип Ле-Шателье.

Если изменить одно из условий, при которых система находится в равновесии, то в системе усилится та реакция которая противодействует производственному изменению. На конденсированные системы давление существенного влияния не оказывает.

N₂ + 3H₂ = 2NH₃

Будем рассматривать гетерогенные системы, много-компонентные, в которых протекают химические процессы.

С термодинамической точки зрения существуют системы изометрий закрытые. В изомерных массообменах термическая и барическая связь отсутствует. Критерием самопроизвольно протекающих процессов изомерных систем может служить изменение энтропии, как было показано, этот критерий для закрытых систем не годится, так как в закрытых системах массообмена нет, но существует термическая и барическая связь. В таких системах V, Р, С являются контролируемыми величинами, и в качестве критерия самопроизвольности процесса обычно пользуются термодинамическим по­тенциалом F, G.

;

В случае протекания химического процесса изучение системы начинают с его фазового состояния – правило фаз Гиббса.  По этому правилу определяют число степеней свободы – число параметров, которые можно изменить, чтобы число фаз не изменялось. Это число свободы не контролируется в ходе процесса.

В связи с тем, что в ходе химического процесса фазовое равновесие и фазовое состояние не нарушается, такие понятия как активность и летучесть можно использовать и при рассмотрении химического равновесия.

Обычно для грубой оценки возможности простого химического процесса используются величины теплового эффекта. Однако такая оценка является в большинстве случаев не совсем точной, так как известно много реакций идущих с поглощением тепла, поэтому наиболее правильно следует в качестве критерия считать , .

;   (1)

Самопроизвольный процесс возможен, если  и. Когда эти величины больше нуля: 1. ; , т.е. в случае экзотермического процесса; 2. , , , , т.е. реакция будет идти за счет энтропийного члена.

Это может иметь место в том случае, если , т.е. когда будет иметь место расширение в процессе реакции.

Вывод: в общем случае не могут величины тепла процессов являться критериями самопроизвольности процессов.

Чтобы ответить на вопрос, при каких условиях энтропийным членом мoжно пренебречь, надо рассмотреть уравнение (1).  можно пренебречь, если тепловой эффект будет очень велик; при малых Т, если реакция будет протекать в твердой или жидкой фазе.

Раскроем смысл всех величин уравнения (1):

;;

Т.о., для нахождения  необходимо знать тепловой эффект реакции данной Т, саму Т, найти .

Существуют три способа нахождения .

1. Исходим из сотоношения (1) и третьего начала термодинамики.

2. Основан на уравнениях изотермы, изобары и изохоры Вант-Гоффа.

3. Базируется на определении ЭДС гальванических элементов.

Третье начало термодинамики.

Она состоит из теоремы Нерста и постулатов Планка.

Теорема: согласно теореме, при, , .

Постулаты: при, само значение , т.е. энтропия правильного кристаллического вещества при Т абсолютном  = 0.

Постулаты Планка не распространяются на все твердые вещества.

Неправильно построенные и аморфные тела не дают нулевой энтропии, однако энтропия их при абсолютном нуле не невелика, т.о. абсолютное значение величины  ни при каких условиях нам неизвестны, известно только их изменение, в то время как можно определить абсолютное значение . Это происходит потому, что нет точек отсчета для нахождения этих термодинамических величин. Величина S для индивидуальных веществ может быть найдена при Т = 0.  "0" – обозначает, что данное значение энтропии абсолютное и отсчитанное от 0, индекс Т показывает температуру, существует специальная таблица с абсолютными значениями энтропии .

Чтобы использовать соотношение (1) ; находим :

абсолютное значение энтропии было найдено следующим образом:

Известно, что:

; ; ;

но, в соответствии с третьем началом термодинамики, последнее уравнение можно преобразовать для идеально твердого тела, если принять = 0.

Это уравнение дает возможность рассчитать абсолютное значение энтропии.

Зная энтропию для твердого тела, можно найти энтропию для жидких и газообразных веществ. Это практически делается так:

       1           2        3             4           5

1 – обозначат энтропию твердого вещества, далее, при переходе веществ в жидкое состояние, энтропия возрастает на величину приведенной теплоты, появляется 2 член.

В подинтегральную величину входит теплоемкость – С; затем идет испарение жидкости при Р = const.

Делается это следующим образом:

такие зависимости строятся для каждого вещества, участвующего в реакции.

п	45,1
ж	16,7
г	31,2
С алм	0,58
С граф	1,36

По выше приведенной форме находят энтропию, зная абсолютное значение энтропии на :

.   рассчитано по аб­солютному значению S.

Недостатком этого метода является то, что необходимо знать значение С всех участвующих в реакции веществ до абсолютного нуля.

Второй способ основан на уравнениях изотермы Вант-Гоффа.

Вывод изотермы Вант-Гоффа.

Для такой реакции необходимо вычислить  реакции, = -.

Изменения изобарного потенциала реакции при условии постоян­ства Р , Т определяется, как известно, следующим равенством:

; ; ;

;

Это не исходные вещества, а активности всех веществ до начала реакций. В начальный момент все вещества берутся в произвольных концетрациях. Если реакция закончившаяся, то наступило состояние химического равновесия, то активности и концентрации всех веществ будут другими, отвечающие, этому состоянию равновесия. В состояния равновесия = 0.

 тогда

Это уравнение называется уравнением изотермы Вант-Гоффа. Это уравнение, позволяет определить максимально полезную работу при какой-то постоянной Т, если известны активности, концентрация, и Р всех веществ до начала реакции и после нее.

 – это работа или энергия, следовательно каждый член в правой части есть А или энергия. 1 член указывает энергию или A в равновесном состоянии;2 член указывает в исходном состоянии. Если реакция находится в равновесии, то для члена такой системы  = 0, эти два члена равна между собой. Если >0, то , следовательно прямой процесс невозможен, возможен обратный процесс;  – прямой процесс возможен.

Чтобы сравнить друг с другом различные реакции, необходимо исходное состояние выбрать одинаковое. За стандартное состояние выбрали, когда активности всех участвующих веществ в реакции равно1.

это стандартная изотерма Вант-Гоффа.

В нашем примере  равновесия выражается через активность, но она может быть выражена через концентрацию , , . Покажем связи между ними.

Законы действия масс в обратимых реакциях. Константа химического равновесия и её выражение. Зависимость константы равновесия от температуры, уравнение Гиббса-Гемгольца, изобары, изохоры Вант-Гоффа.

Согл-о , , , ;

Покажем связь  и :  (2); ; с учетом уравнения (2):

.

Выразим  (константа мольной доли). Выразим мольную долю для каждого вещества.

; ; ; ;

Как выразить  (константу выраженную через давление)?  Чтобы найти связь между  и  выразим константу мольной доли.

Р – общее давление в системе.

в случае , :

.

Если рассматриваем сложную систему, в которой участвуют жидкие, твердые и газообразные вещества, то как правило: для твердых веществ используются активности, для веществ в растворе – концентрации, для газов – летучесть и постоянное давление.

Зависимость и константы равновесия от температуры.

Очень часто возникает необходимость расчета и константы равновесия при каких-то больших температурах, зная  и константу равновесия при определенной температуре.

Эта зависимость дается уравнениями Гиббса-Гельмгольца изобарно-изотермического Вант-Гоффа.

; .

С другой стороны согласно четвёртому объединенному уравнению: ;  по определению  – уравнение Гиббса-Гельмгольца

Это уравнение позволяет найти зависимость от температуры.

 – является температурным коэффициентом полезной работы.

Выведем уравнение изобары Вант-Гоффа, для этого уравнения Гиббса-Гельмгольца рассмотрим в таком виде: , поделим левую и правую часть на :

; .

 – подставим в последнее уравнение.

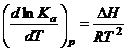;  – изобара Вант-Гоффа.

Если исходишь из уравнения изохорно-изотермического потенциала то можно прийти к изохоре Вант-Гоффа.

 – третье объединенное уравнение.

Чтобы найти зависимость константы от Т, уравнение Вант-Гоффа нужно проинтегрировать.

Если подставить в эту производное значения V,U,H,F,G то мы получим пропорциональные мольные величины.

рассмотренных термодинамических параметров. Мы знакомы с первой парциальной мольной величиной, а именно с химическим потенциалом  – есть парциальная мольная величина. Покажем это.

Мы знаем, ,  – функция состояния, поэтому

;

при Р, Т = const: .

В данном случае понятие химического потенциала и парциальной мольной величины совпало.

Физический смысл химического потенциала есть парциально мольная величина изобарно-изотермического потенциала.

Пусть мы имеем смесь, которая содержит большее количество молей вещества; прибавим 1 моль вещества, это существенно не изменит ни Р, С, V, будет происходить только изменение изобарно-изотермического потенциала, который будет равняться пропорциональному молю данного вещества в смеси. Это изменение и является химическим потенциалом смеси.

Химический потенциал, выражающийся через другие термодинамические функции, не является парциальной мольной величиной.

Не всякая частная производная по компоненту является парциальной мольной величиной.

1 случай. , следовательно левая часть меньше нуля, это значит, что  с увеличением Т уменьшается, а чем меньше константа , тем меньше концентрация продуктов реакции , т.е. при увеличении Т, когда  равновесии реакции сдвигается в сторону исходных веществ. Это находится в соответствии с принципом Ле-Шателье.

По законам кинетики с повышением Т, повышается скорость реакции, и приходится выбирать оптимальный режим работы, чтобы выход продуктов был максимальный и скорость достаточной.

2 случай. , левая часть меньше нуля, следовательно  растет с увеличением Т.  увеличивается, увеличивается концентрация продуктов, т.е. равновесие смещается в сто­рону прямой реакции. В данном случае влияние на Т, кинетику и термодинамику одинаково.

Приближенное и точное интегрирование изобары Вант-Гоффа.

При приближенном интегрировании Т невелика, величина постоянная и не зависит от Т.

;;

Зная К при какой-то  можно определить К при какой то температуре .

Мы нашли определенный интеграл ,найдем неопределенный.

; ; .

Точное интегрирование.

При точном интегрировании в широком интервале Т, необ­ходимо учитывать зависимость теплового эффекта (зависимость дается уравнение Кирхгофа).

; ; ; ;

;;

Константа интегрирования находится следующим образом, взяв  при Т = 298 из таблицы, подставим затем в последнюю формулу и определим при любой температуре, затем подставляем значение  при этой температуре в уравнение изобары вант-Гоффа

Константа находится так, как показано выше. Константа  находится аналогичным способом – сначала подставляем const при Т = 298. Затем К находят при нужной Т. Зная константу при нужной Т, можно найти зависимость изобарно-изотермического потенциала при любой Т.

 позволяет определить зависимость  от какой-то Т.

Зная эту зависимость, можно найти зависимость максимально полезной А от Т.

Достоинства.

Может применятся к любым реакциям. Позволяет рассчитать при любых температурах, даже очень высоких.

Может оказаться, что влияние Т во многих случаях настолько больше, что может  меняться К, ,но и знак этих величин, т.е. процесс может изменить направление.

Недостатки.

Необходимо знание константы интегрирования и значение , К при температуре 298.