Элементы статистической термодинамики.

Энтропия и неупорядоченность состояния системы.

Второй закон т/д имеет статистический характер. Он утверждает существование некоего свойства системы S связанного с теплообменом и T при которой  этот теплообмен происходит. Соотношение  или для изолированной системы  были введены Клаузиусом и являются математическим выражением закона №2 т/д. Свойства системы S было названо энтропией, а второй закон т/д показывает, что приращение энтропии или равно приведенной теплоте для равновесно – обратимых процессов или больше ее для процессов неравновесных. То энтропия оказывается свойством системы, связанным с одной стороны теплообменом, с другой необратимостью. Эта дуалистичность помогает разобраться в S не с классических позиций Клаузиуса, а с точки зрения развитой позже молекулярной статистики. Дуалистичность энтропии можно понять, если использовать представления об атомно-молекулярном строении материи и рассматривать состояния системы с точки зрения упорядоченности – неупорядоченности движения или состояния, составляющих систему частиц. Примером упорядоченности молекулярной структуры может служить правильно сформированный кристалл чистого свойства при . В таком кристалле атом размещается в узлах кристаллической решетки, около которых они совершают одинаковые колебательные движения с нулевой энергией. Энтропия такого кристалла по Планку равна 0 (3-й закон т/д). Идеальный порядок нарушается, если тело поглощает теплоту и нагревается.

Нарушение упорядоченности связанное с нагревом ведет к увеличению S

, С-теплоемкость

Фазовые переходы, связанные с разрушением кристалла (плавлением) сопровождаются изотермическими поглощением теплоты и резким возрастанием S вещества.

   

DS_исп>>DS_пл ,т.е. при образовании наиболее коотизированного состояния (пара или газа) возрастание S более интенсивно.

Процессы фазового перехода проведены в условиях равновестности и дает значение 2-а закона т/д использованого для них со знаком равенства. Но увеличение S системы возможно и без теплообмена при протекании неравновесного процесса. Пример – замыкание аккумулятора на сопрот. в изолиров. системе, когда электрическая энергия превращается в теплоту Джоуля без совершения работы. При этом неупорядоченность молекулярного состояния системы увеличивается, S возрастает =>S можно рассматривать как меру неупорядоченности молекулярного состояния системы. Эти качественные представления количественно развивает статистическая термодинамика. Она является частью более общего раздела науки – статистической механики (конец 19 века основные положения Больцман – Гиббс).

Микросостояния и ансамбли Гиббса.

Состояния системы в т/д определяемое ее свойствами – P, V и T будем называть макросостояниями системы. От макросостояний следует отличать микросостояния – которое характеризуется мгновенными значениями всех зависящих от времени переменных N составляющих систему частиц. В общем случае для описания положения в пространстве частицы (многоатомной молекулы) требуется f обобщенных координат; q – обобщенная координата.

q1(t), q2(t)…..qf(t), t – время.

И столько же сопряженных с ними импульсов Pi(t), i=1,2,3…f.

Многомерное пространство с 2f-координатами называется m-пространство – пространство молекулы. Точка в таком фазовом пространстве будет представлять состоянием частицы в момент времени T. А изменение этого состояния во времени изобразиться некоторой траекторией движения. Для газа, содержащего N многоатомных молекул фазовое пространство имеет уже 2Nf измерений и называется g-пространством (пространством газа). Точка в таком пространстве изображает мгновенное состояние всей системы в целом, а траектория определяется ур-ями вида

qi=q(t) u pi=p(t) , i=1,2,3…Nf которые определены ур-ями движения Гамельтона.

          

Краткая запись этих ур-й H(q,p) – ур-е Гамильтона.

Если система находиться в равновесии, то ее макросостояние не измен. во времени, но микрооненич. порционные могут меняться непрерывно, но так, чтобы макросостояние оставалось неизменным. Поэтому с классической точки зрения должно существовать бесчисленное множество микросост., совместимых с макроскопической характеристикой т/д системы.

Для изучения статистического поведения т/д систем Гиббс предложил метод ансамблей.

Ансамбль Гиббса – большой ряд микросостояний, совместимых с данным макросостоянием. Ансамбль можно представить как очень большое число ( в ) аналогичных т/д систем, но находящихся в различных стадиях развития, т.е. в различных микросостояниях. По аналогии с понятием т/д изолированных, закрытых и открытых систем, в зависимости от поставленной задачи применяют различные ансамбли. В соответствии с ограничениями, налогаемыми на т/д систему. Наиболее важным типом ансамблей являются микроканонический, канонический и большой канонич. Микрока­нонический и канонический названы малыми ансамблями. Микроканонический ансамбль соответствует изолированной системе, которая не может обмениваться с окружением ни веществом ни энергией. Она характеризуется каноническим ансамблем соотв. закрытой изотермической системе с постоянными значениеми V,N,T. Такая система находиться в термическом равновесии с окружающей средой и может обмениваться с ней энергией, но не вещ-вом. Он оказался наиболее удобным для цепей статистической т/д. Большой канонический ансамбль соответствует открытой изотермической системе,которая характеризуется  V, T, m. Он находиться как в тепловом так и в материальном равновесии со средой, может обмениваться с ней в-вом и энергией.

Развитие во времени микроскопич динамического состояния кажлого члена малого канонического ансамбля будет описываться траекторией, изображающей точки в 2 Nf-мерном фазовом пространстве. Если же в том же пр-ве находятся изображенные точки других членов ансамбля, то получается как бы облако движущихся изображающих точек. Мгновенная плотность облака в данной точке характеризуется нормированной ф-ей распределения

r(qi,oi)  ,i=1,2,3,…,Nf

Величину следует понимать, как долю от общего числа систем в ансамбле, приходящегося на единицу гиперобъема фазового пространства. В области точки вероятность, что изображающая точка произвольно взятой системы из ансамбля окажется в какой-то единице V фазового гиперпространства.

Подсчет микросостояний по Больцману.

В системах, состоящих из большого числа одинаковых молекул (1 моль газа) для описания механического состояния применяются фазовое m пространство 2f измерений, если f – число степеней свободы молекулы. В таком пространстве каждая точка будет определять координаты и импульсы данной молекулы. Число изменений в g – пространстве при описании состоянии всей системы в целом будет в N раз больше, если N – число молекул в системе. Если между молекулами системы практически отсутствует сила взаимодействия, то g – пространство системы можно представить совокупностью m пространств.

В классической статике Больцмана макросостояния системы например любого идеального газа характеризуются числом фигуротивных точек в различных ячейках фазового пространства. Молекулы считаются различными и обмен местами двух молекул находящихся в различных ячейках даст новое микросостояние фаз изменение микросостояния. f .o. число микросостояний соотв. данному макро можно подсчитать путем нахождения числа способов размещения фигуративных точек по ячейкам. Пусть систе­ма состоит из N молекула, а ее макросостоянию соответствует N_i точек в i – ячейке. Т.к. перестоновки внутри ячейки не считаются т.к. они не дают новое микросостояние, то число микросостояний находится как число перестановок с повторениями.

, число G подсчитанное по этой формуле называется числом комплексий.

Термодинамическая вероятность и энтропия.

Основные положения т/д статистической механики даются в виде постулатов.

Первый: постулат равной вероятности, второй – теорема о средних значениях.

1 Постулат: для изолированоой системы все достижимые области фазового пространства имеют равные априорные вероятности (исходные). Иначе говоря для микроканонич ансамбля изображающие точки распределены равномерно по достяжении фазового пространства.

2 Постулат: ТЕОРЕМА: среднее по времени значения физически наблюдаемой величины F(q,p) для системы равно среднему значению физически наблюдаемой величины по ансамблям.

Это следует из того,что каждая система ансамбля в течении достаточно долгого времени будет приходить в состояние каждого другого члена ансабля. Т.о. средних значениях позволяет установить точные связи между т/д переменными и механическими макроскопическими характеристиками. Так, каждое т/д свойство q под которым можно подразумевать p, энергию, S определяется как среднее по времени некоторой динамической переменной q(q,p). Это можно выразить так:

, причем

Среднее по ансамблю выражается:

Тогда теорема о средних значениях записывается так, .

Это имеет смысл только для систем, состоящих из достаточно большого числа достаточно взаимодействующих частиц, которые называются эргоидными системами. Из постулатов равной вероятности следует,что все микросостояния системы, совместимы с заданными условиями, например с постоянством энергии математически равновероятные. Представление о микросостояниях, их равной вероятности и о том что различным макросотояним может соответствовать различное число микросостояний ведет к понятию т/д вероятности макросостояния обозначаемой W

Т.о. т/д вероятность состояния пропорциональна числу микросостояний, соответствующих данному макросостоянию. Коэффициент пропорциональности можно положить равным 1 и рассматривать W  как относительную вероятность по отношению к вероятности стандартного состояния. Кроме того W можно рассматривать как числитель математическую вероятность, в знаменателе которой стояло бы число всех мыслимых для данной системы микросостояний, совместимых с законами сохранения.

Т.о. W=G³1 Для обычных молекулярных систем в равновесном состоянии W очень велико. Согласно Больцману статистический смысл 2-го закона тд состоит в том, что изолированная система развивается в направлении большей т/д вероятности. Т/д вероятность равновесного состояния для обычных молекулярных систем например для 1-го моля газа, во много раз больше чем сумма т/д вероятностей всех возможных неравновесных состояний:

Равновесное состояние соответствует наибольшему состоянию W. Таким же образом меняется и энтропия изолированной системы, поэтому ее можно считать функцией W.

S=f(W)

Для установления вида этой ф-ии рассмотрим 2-е независимых системы свероятностями состояний W1 и W2. Т/д вероятность сложной системы, составленной из этих двух выразиться произведениями:

Энтропия отдельных систем: S1=f(W1) u S2=f(W2)

А энтропия суммарной системы  в силу аддетивности данного экстенсивного св-ва системы.

, дифференцируем по W1 u W2:

 или

         

                

                  

 При сравнении данного выражения с определением d как функции W можно видеть, что const=0. Получаем уравнение Больцмана:

S=k ln(W)

Впервые в таком виде это ур-е было получено Планком в 1900 г. Оно лежит в основе статистической т/д, k- произвольна, но ее желательно выбрать так, чтобы энтропия, определяемая этим ур-ем, совпадала бы с обычной энтропией 2-го закона, связанного с теплопередачей.

С этой целью рассмотрим процесс изотермического расширения идеального газа от V₁  до V₂.

, где W₁ и W₂ – вероятнояти пребывания 1-ой молекулы с V₁ и V₂. Эти ве­роятности относятся также как сами эти V, т.е. W₂/W₁=V₂/V₁. Если молекулы 2-е, то  А для одного моля газа N_A молекул и . Таким образом  для 1-го моля газа: , но для идеального газа имеет место:  и , k- Постоянная Больцмана.

При статистическом толковании S системы, как меры неупорядоченности ее состояния при поглощении теплоты следует рассмотреть вопрос о Тепловой Смерти Вселенной.

Один из основоположников классической т/д Клаузис дал следующюю форму­лировку 1-го и 2-го законов т/д:

Энергия мира постоянна (не вызывает сомнения в связи отсутствия сведений об отклонении от закона сохранения энергии)

Sмира ® max

Относительно 2-го возникли разногласия: Клазиус, распространяя на всю вселенную закон увеличения S для самопроизвольных процессов в изолированной системе, приходит к неизбежному выводу о стремлении мира к равновесию, когда выравниваются P, T, - тепловая смерть Вселенной.

Признаки неизбежного конца вселенной ведет к допущению ее лагл, возникновению или акта творения. Это противоречит материалистической ф-ии, подтверждая идеалистич. Поэтому до настоящего времени остается незавершенности физического решения этой проблемы. Не вдаваясь в обсуждение характера завершения представлений относит характера вселенной. Всетаки можно придти к выводу о совершенно иных масштабах и физ. сущности космических явлений по сравнениюс огромными земными наблюдениями, для которых и установлен 2-й закон т/д.

Закон распределения молекул по энергиям. (З-н Больцмана).

Методы статистич т/д позволяют вычислить т/д ф-и системы, состоящие из большого числа молекул на основе характеристик молекул, полученных спектроскопическим, электрографическим, рентгено и другими методами.

Кроме того эти методы значит роль играют в хим кинетике и в первую очередь в статистич. расчете скорости р-ции. (теория абсолют скоростей)

В основе этих методов лежит закон распред. мол. по энергиям

ВЫВОД: Для вывода з-на рассмотрим газообразную систему которая состоит из очень большого числа N молекул. Сист обладает энергией U и занимает постоянный объем V, т.е. находит в условиях U=const, V=const, такая система с т/д точки зрения изолированна. Все молекулы ее химически идентичны, но могут обладать различными энергиями. В простейшейм случае это будет энергий поступательного движения , где m-масса, c-скорость движения частиц.

Распределение молекул по энергиям дается указанием чисел молекул, обладающих определенной энергией. N₁ с энергией e₁

N₂ с энергией e₂ и т.д.

Полная энергия рассматриваемой системы выразиться суммой:

Постоянным будут также число молекул åNi=const . согласно квантовой механике одной и той же энергии молекулы может отвечать несколько gi собственных состояний. В связи с этим можно с почти одной и той же величиной ее. Такие кратные уровни называют выражденными. А степень выраждения gi – статистическим весом уровня или его суммарной вероятностью

Макросостояние системы однозначно определяется распростронением неразличимых молекул по энергиям. Т/д вероятность состояния запишем сначала число способов распределения N молекул по i-группам.

Внутри каждой группы Ni различаемых молекул могут размещаться по gi уровням.

Одну молекулу можно разместить по gi уровням gi способами. 2 молекулы – способами и т.д. => для Ni молекул число способов размещения будет .  Полное число макросостояний, т.е. т/д вероятность данного макросостояния W получиться умножением найденного числа распределения по группам на числа распределения внутри групп.

Равновесному состоянию изотермической системы с т/д точки зрения отвечает max энтропии. А со статистической – max т/д вероятности. Связь между S u W дается формулой Больцмана:

ЧислаN u Ni  всегда слишком велики поэтому к факториалам можно применить формулу Стирлинга, которая тем точнее, чем больше N.

или в логарифмической форме

При больших N первый член в правой части равенства можно отбросить.

Тогда При равновесии значения S u W – max => дифференциалы:

Частные изменения S будут:

 Тогда условием равновесия будет равен­ство:  (*)

Используя 2-а ур-я связи:  можно выразить две из вели­чин dNi как ф-и всех остальных. Поэтому независимыми будут все изменения Ni крому 2-х. Чтобы избавиться от зависимости изменений используем метод неопре­деленных методов Лагранжа. Для этого умножим dN u dU соотв. на l и m и суммируем с (*)

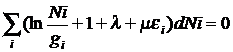 Производные множ. l и m подбирают так, чтобы 2 из коэффициента при dNi равнялось 0

Пусть  и

Тогда в сумме останутся лишь слагаемые, содержащие независимые вариации чисел dNi. В этом случае общее равенство будет равно 0, если каждый из (i-2) коэф. тоже равен 0. Т.о для изолированной равновесной системы, состоящей из N слабовзаимодей­ствующих молекул справедливо равенство.

Уравнение Больцмана.

Полученное выражение – общий вид закона распределения молекул по энергиям в классической статистике Максвелла-Больцмана. Для получения конкретного вида распределения необходимо найти В и m.

Для этого сложим все числа молекул.

, откуда

;

, с учетом U и N:

 или

 дифференцируем по S при V=const последний член не зависит от S

,

 Тогда уравнение Максвелла-Больцмана можно представить: Эта формула – выражение закона распределения Больцмана, которое читается так:

Для молекулярной системы, находящейся в равновесии, число молекул, обладающих энергией e_i пропорционально множителя Больцмана »e^e/kT.

Определение молекулярной суммы

по состояниям.

С учетом выражения закон Больцмана запишем в виде:

 или

 – молекулярная сумма по состояниям – сумма множителей Больцмана, записанных для всех возможных энергетических состояний молекул. Если назвать состояние молекулы с наиболее низкой энергией нулевым, то сумма по состояниям отдельной молекулы в развернутом виде записывается так:

,

где суммируются все возможные энергетические состояния молекулы. При записи закона Больцмана сумму по состояниям можно рассматривать как обобщенный множитель Больцмана, характеризующий полное число молекул данного вида в системе.

.

Сумма по состояниям не имеет размерности и помогает описать в удобной математической форме распределение энергии между молекулами в системе.