Лекция 15.

Поступательная сумма по состояниям и ее вклад в термодинамические свойства.

Основное уравнение статистической термодинамики F = U_o – klnz позволяет выразить все термодинамические функции через величины, характеризующие свойства молекул. Чтобы рассчитать суммы по состояниям и с их помощью найти различные термодинамические свойства, необходимо вычислить теоретически или определить на опыте энергетические уровни системы в целом, в общем виде это пока не возможно. Уравнения квантовой и классической механики определяют лишь уровни энергии, отвечающие отдельным составляющим молекулярного движения, а именно: поступательного, колебательного, вращательного, электронного и ядерного возбуждения. Т.о., энергия молекулы идеального газа выражается формулой:

e = e_пост. + e_кол. + e_вр. + e_эл. + e_яд.

В этой сумме все члены, кроме первого, отвечают внутримолекулярной энергии и взаимосвязаны. Энергия поступательного движения не зависит от других видов движения и наоборот, поэтому полную энергию можно записать: e = e_пост. + e_{внутр.­}, а соответственно молекулярная сумма по состояниям: z = z_пост × z_внутр.. Для расчета суммы по состояниям при не слишком высоких температурах прибегают к упрощениям. В первом приближении считают, что все внутримолекулярные виды энергии не зависят друг от друга – приближение Борна-Оппенгеймера, в этом случае для полной суммы по состояниям будем иметь: : z = z_пост × z_кол. × z_вр. × z_эл. × z_яд. , т.е. z факторизуется по отдельным видам движения.

Поступательная сумма по состояниям (поступательное движение).

Для определения поступательной суммы по состояниям необходимо использовать уравнение, описывающее поступательную энергию частиц, в отсутствии потенциальных полей энергия движения частиц – это кинетическая энергия. В классической механике она определяется: .

Квазиклассическая сумма по состояниям для трех степеней свободы поступательное движение одной частицы выражается через многомерный интеграл: 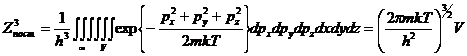, т.к. , , при .

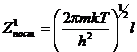, l – линейный размер системы.

         Согласно квантовой механике для частицы в ящике с ребром l энергия системы для одной степени свободы вычисляется из уравнения Шредингера:

,

общее решение: , при х = 0 и х = l ®

при  и B = 0 ®

  , где n_x = 1,2… - квантовое число, определяющее дозволенные значения энергии частицы, движущейся параллельно оси х.

Т.о., одномерные поступательные движения оказываются квантованными, и это дает квантовую поступательную сумму по состояниям в виде:

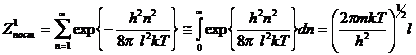 , что полностью совпадает с выражением для Z¹ в квазистатистическом случае.

         Для частицы в потенциальном поле U (x,y,z) полная энергия запишется:  в этом случае поступательная сумма по состояниям: ,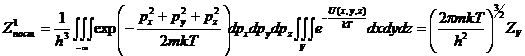

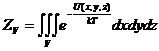- конфигурационный интеграл.

         Если потенциальная энергия U (x,y,z) – это энергия внешнего поля (напр., гравитационного), то вычисление Z_V достаточно просто;  если же необходимо учесть энергию межмолекулярных взаимодействий, то нахождение конфигурационного интеграла становится трудной задачей, т.к. она связана с вычислением кратного интеграла по координатам множества частиц: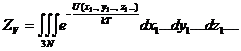

         Итак, поступательная сумма по состояниям для идеального газа в целом будет являться большой суммой по состояниям:

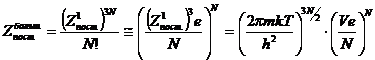
с помощью данного уравнения вычисляют поступательную составляющую термодинамических функций для многоатомных идеальных газов.

1. Средняя энергия поступательного движения:

2. Давление, через которое выражается уравнение состояния идеального газа:

, уравнение состояния: pV=NkT

3. Поступательная составляющая энергии Гельмгольца:

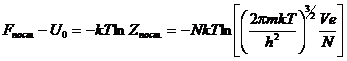
4. Поступательная составляющая энтропии:

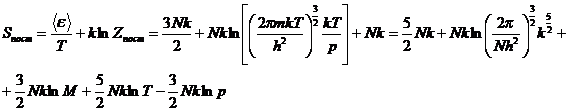
где

Тогда с учетом всего этого можно получить уравнение Закура и Тетроде:

S_пост=Rln(M ^3/2T ^5/2)-RlnP_(атм)-2,31 кал/моль∙К

 

Это уравнение определяет абсолютную энтропию, т.к. в него входит явно h, что соответствует использованию квантово-химического подхода и подхода для многих простых газов (N₂, O₂). Поступательная энтропия по абсолютной величине заметно превышает вклад внутренних степеней свободы и является основной составляющей энтропии газа.

Деление на N! при вычислении поступательной суммы по состояниям дало более точное значение для энтропии, чем в классической термодинамике, т.к. в уравнении Закура не появляется избыток энтропии и энтропия смешения газа с самим собой, которая равна нулю. (Классической выражение: S=S(T)+NkTlnV=nS^o(T)+nRlnV)